Problem solving Notes

Big O
- If we have two functions and we need to find which is optimal. We can use Big O to find the one.
- We can easily classify the functions from Great → Awful
- It's not only about make it work we should also care about make it best. Big O will help.
- Good to have a vocabulary to talk about how our code performs.
- To discuss tradeoff between different approaches
- Help to identify the inefficient code causing the crashes.
- Timing the code by checking how long it takes to run is a bad idea.
- Counting how many operation the function doing is not great. Like calculating the operation of a = a*b+c this is not good 😌. We can't calcualte the operation inside look etc.
- We should calculate the overall calculations.
  💡 Big O Notations is a way to formalize fuzzy counting. It allows us to talk formally about how the runtime of an algorithm grows as the inputs grow.
  We say that an algorithm is O(f(n)) if the number of simple operations the computer has to do is eventually less than a constant times f(n), as n increases
  f(n) could be linear (f(n) = n) f(n) could be quadratic (f(n) = n2) f(n) could be constant (f(n) = 1) f(n) could be something entirely different!
  O(1) ⇒ Runtime won't grow based on the input
```
function addUpTo(n) {
  return (n * (n + 1)) / 2;
}
// Always 3 operations
```
  O(n) ⇒ Runtime grow based on the input
```
function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {}
}

// Number of operations is (eventually) bounded by a
// multiple of n (say, 10n). In short, O(n)
```
```
function countUpAndDown(n) {
  for (let i = 0; i < n; i++) {
    console.log(i);
  }
  for (let j = n - 1; j >= 0; j--) {
    console.log(j);
  }
}

// Number of operations is (evenutally bounded by a multiple of n (say, 10n)
// We can simply by O(n)
```
  O(n2) ⇒ Runtime grow twice the input
```
function printAllPairs(n) {
  for (var i = 0; i < n; i++) {
    for (var j = 0; j < n; j++) {
      console.log(i, j);
    }
  }
}
```

SImplification

No matter what input is it'll run exact operation

O(500) ⇒ O(1) so, we can simplify like this.
O(2n) ⇒ O(n)
O(13n2) ⇒ O(n2)
O(n + 10) ⇒ O(n) - n + 10 constant operation will result in O(n)
O(1000n + 50) ⇒ O(n)
O(n2 + 5n + 8) ⇒ O(n2)
Some more tips:
1. Arithmetic operations are constant (adding, sub, div, etc)
2. Variable assignment is constant (a =3455, etc)
3. Accessing elements in an array (by index) or object (by key) is constant
4. In a loop, the complexity is the length of the loop times the complexity of whatever happens inside of the loop
Examples:
```
function logAtLeast5(n) {
  for (var i = 1; i <= Math.max(5, n); i++) {
    console.log(i);
  }
}

// O(n)
```
```
function logAtMost5(n) {
  for (var i = 1; i <= Math.min(5, n); i++) {
    console.log(i);
  }
}

// O(1)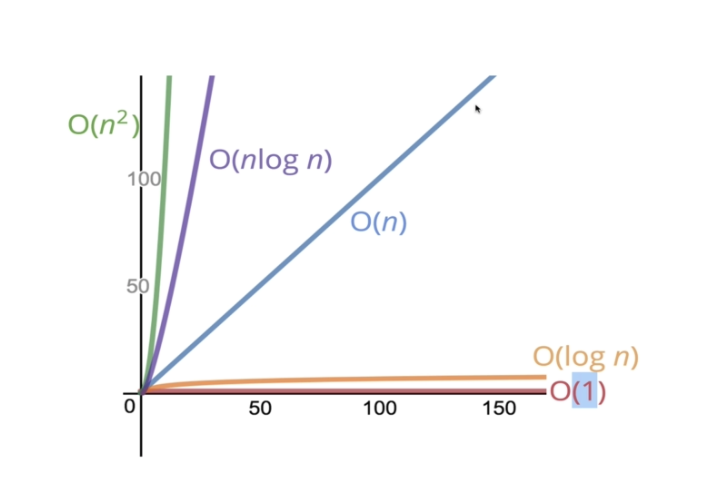
```

`O(1)` time

Accessing Array Index (int a = ARR[5];)
Inserting a node in Linked List
Pushing and Poping on Stack
Insertion and Removal from Queue
Finding out the parent or left/right child of a node in a tree stored in Array
Jumping to Next/Previous element in Doubly Linked List

`O(n)` time

In a nutshell, all Brute Force Algorithms, or Noob ones which require linearity, are based on O(n) time complexity

Traversing an array
Traversing a linked list
Linear Search
Deletion of a specific element in a Linked List (Not sorted)
Comparing two strings
Checking for Palindrome
Counting/Bucket Sort and here too you can find a million more such examples....

`O(log n)` time

Binary Search
Finding largest/smallest number in a binary search tree
Certain Divide and Conquer Algorithms based on Linear functionality
Calculating Fibonacci Numbers - Best Method The basic premise here is NOT using the complete data, and reducing the problem size with every iteration

`O(n log n)` time

The factor of 'log n' is introduced by bringing into consideration Divide and Conquer. Some of these algorithms are the best optimized ones and used frequently.

Merge Sort
Heap Sort
Quick Sort
Certain Divide and Conquer Algorithms based on optimizing O(n^2) algorithms

`O(n^2)` time

These ones are supposed to be the less efficient algorithms if their O(nlogn) counterparts are present. The general application may be Brute Force here.

Bubble Sort
Insertion Sort
Selection Sort
Traversing a simple 2D array

Space Complexity

1. Most primitives (booleans, numbers, undefined, null) are constant space
2. Strings require O(n) space (where n is the string length)
3. Reference types are generally O(n), where n is the length (for arrays) or the number of keys (for objects)

```jsx
function sum(arr){
 let total = 0; // Variable declaration
 for (let i = 0; i < arr.length; i++) { // Variable declaration
  total += arr[i];
 }
 return total;
}
// O(1) space
```

```jsx
function double(arr) {
 let newArr = []; // Space will grow proportional to the input
 for (let i = 0; i < arr.length; i++){
  newArr.push(2 * arr[i]);
 }
 return newArr;
}

// O(n) space
```

Linear Searching
💡 A linear search or sequential search is a method for finding an element within a list. It sequentially checks each element of the list until a match is found or the whole list has been searched.
A simple approach is to do a linear search, i.e
- Start from the leftmost element of arr[] and one by one compare x with each element of arr[]
- If x matches with an element, return the index.
- If x doesn’t match with any of elements, return -1.
  Time Complexity: Best - O(1)
  Average - O(n)
  Worst - O(n)

Binary Searching

Binary search is a much faster form of search
Rather than eliminating one element at a time, you can eliminate half of the remaining elements at a time.
Binary search only works on sorted arrays!

The idea is Divide and Conquer

Pseudocode

This function accepts a sorted array and a value
Create a left pointer at the start of the array, and a right pointer at the end of the array.
While the left pointer comes before the right pointer:
- Create a pointer in the middle
- If you find the value you want, return the index
- If the value is too small, move the left pointer up
- If the value is too large, move the right pointer down

If you never find the value, return -1

function binarySearch(sortedArray, seekElement, comparatorCallback) {
  // Let's create comparator from the comparatorCallback function.
  // Comparator object will give us common comparison methods like equal() and lessThen().
  const comparator = new Comparator(comparatorCallback);

  // These two indices will contain current array (sub-array) boundaries.
  let startIndex = 0;
  let endIndex = sortedArray.length - 1;

  // Let's continue to split array until boundaries are collapsed
  // and there is nothing to split anymore.
  while (startIndex <= endIndex) {
    // Let's calculate the index of the middle element.
    const middleIndex = startIndex + Math.floor((endIndex - startIndex) / 2);

    // If we've found the element just return its position.
    if (comparator.equal(sortedArray[middleIndex], seekElement)) {
      return middleIndex;
    }

    // Decide which half to choose for seeking next: left or right one.
    if (comparator.lessThan(sortedArray[middleIndex], seekElement)) {
      // Go to the right half of the array.
      startIndex = middleIndex + 1;
    } else {
      // Go to the left half of the array.
      endIndex = middleIndex - 1;
    }
  }

  // Return -1 if we have not found anything.
  return -1;
}

Bubble Sorting
- Sorting is an incredibly common task, so it's good to know how it works
- There are many different ways to sort things, and different techniques have their own advantages and disadvantages.
  Javascript Sorting:
```
["Karthik", "Javascript", "Algorithms"].sort();
// ['Algorithms', 'Javascript', 'Karthik']

[6, 4, 15, 10].sort();
// [10, 15, 4, 6]
```
- The default sort order is according to string Unicode code points. The array is sorted according to each character's Unicode code point value, according to the string conversion of the each element.
- The built-in sort method accepts an optional comparator function
- You can use this comparator function to tell Javascript how you want it to sort
- The comparator looks at pairs of elements (a and b), determine their sort order based on the return value
  - If it returns a negative number, a should come before b
  - If it returns a positive number, a should come after b,
  - If it returns 0, a and b are the same as far as the sort is concerned.
  Bubble sort:
- A sorting algorithm where the largest values bubble up to the top!
  Psuedocode:
  1. Start looping from with a variable called i the end of the array towards the beginning
  2. Start an inner loop with a variable called j from the beginning until i - 1
  3. If arr[j] is greater than arr[j+1], swap those two values!
  4. Return the sorted array
```
function bubbleSort(arr) {
  var noSwaps;
  for (var i = arr.length; i > 0; i--) {
    noSwaps = true;
    for (var j = 0; j < i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        var temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
        noSwaps = false;
      }
    }
    if (noSwaps) break;
  }
  return arr;
}
```
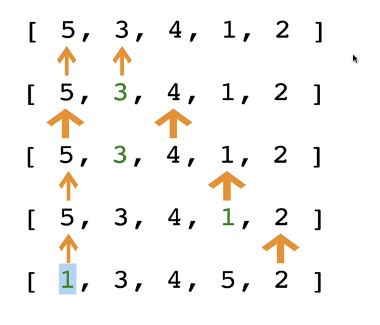
Selection Sort
Similar to bubble sort, but instead of first placing large values into sorted position, it places small values into sorted position.
Pseudocode:
1. Store the first element as the smallest value you've seen so far.
2. Compare this item to the next item in the array until you find a smaller number.
3. If a smaller number is found, designate that smaller number to be the new "minimum" and continue until the end of the array.
4. If the "minimum" is not the value (index) you initially began with, swap the two values.
5. Repeat this with the next element until the array is sorted.
```
function selectionSort(arr) {
  for (var i = 0; i < arr.length; i++) {
    var lowest = i;
    for (var j = i + 1; j < arr.length; j++) {
      if (arr[j] < arr[lowest]) {
        lowest = j;
      }
    }
    if (i !== lowest) {
      var temp = arr[i];
      arr[i] = arr[lowest];
      arr[lowest] = temp;
    }
  }
  return arr;
}
```

Coding Aptitude

SImplification​

Space Complexity​

SImplification

Space Complexity